All wallets have to be upgraded, be among the first to use quantum safe crypto to secure your assets. Click Launch Wallet below. ⬇⬇⬇
Launch Wallet

Hindsight is 20/20

The Future is Coming. Get There First.

The future of your blockchain is the extension of you, your values, and your security. Protect it from quantum threats before it’s too late.

View Demo

The next generation of computers that use quantum mechanics to solve problems too complex for classical computers.

Quantum computers are programmed with quantum circuits that cannot be efficiently simulated with classical computers. They enable shortcuts for issues not possible to solve by classical bits and transistors of our current computers.
Discover More
Play Video

Why Are They a Concern For Blockchain Users

Quantum computers are known to be good at breaking cryptography and simulating quantum systems. While future large-scale quantum computers force us to upgrade the cryptography of current systems today, they will also enable a new industrial revolution and qualitatively expand our ability to design new molecules, drugs, and materials at an exponentially faster rate.

Who They Affect

Practically anyone invested or involved in cryptography is positioned to become a target. Current major blockchains are vulnerable to quantum attacks and once broken, it will be impossible to differentiate between a real wallet owner and a hacker who forged a signature of one. Blockchain businesses, creators, and users are all vulnerable to quantum computing and any data, assets, or investments within the crypto-verse are subject to attack.

Partners

g-logo_3
bigblu-logo_3
git-logo_3
amz-logo_3
The Problem

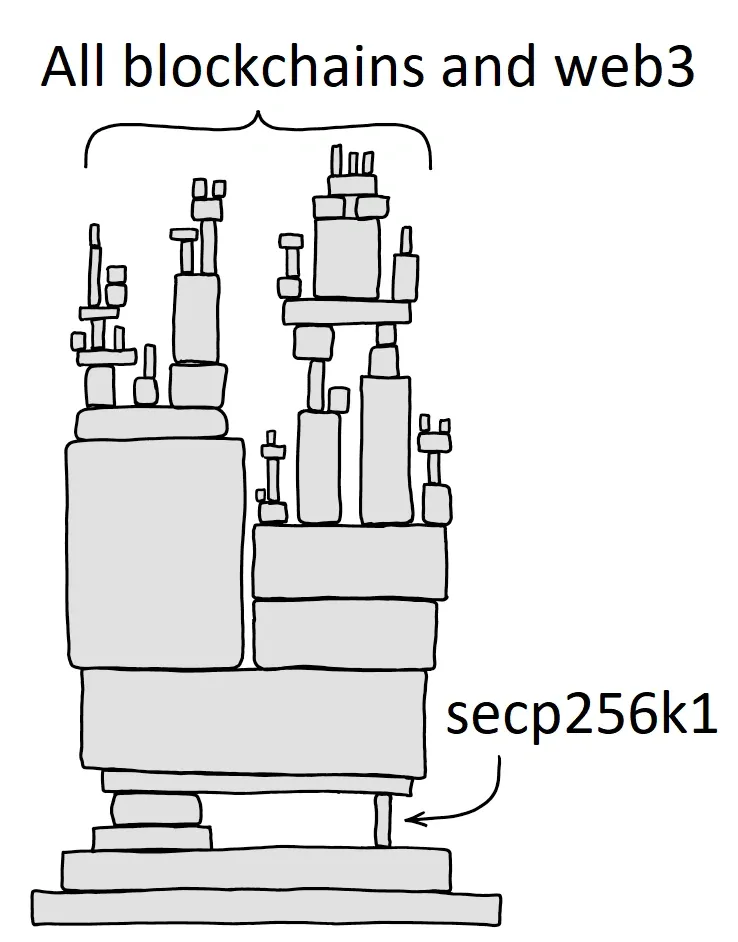
Eliptic curve cryptography is the Achille's heel of web3.

Blockchain Eliptic Curve

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Empirical Risk Assessment

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Current Best Estimates

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Early Fault-Tolerant Experiments

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Projections For Breaking RSA

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

secp256k1

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

The Pauli Group Solution

With great power comes great responsibility.

Quantum Computing Threat

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Solution Implementation

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

Securing Vulnerability

Sollicitudin massa maecenas purus adipiscing egestas natoque fringilla odio ac sodales

The Problem

How To Secure Yourself Against Quantum Computers

To secure funds and digital assets, we’ve built the Anchor wallet that uses well-known methods resistant to quantum computers at the cost of using bigger keys.

Anchor uses the one-time signature scheme of Lamport signatures uses a random number generator and a cryptographically secure one-way hash function to arm your assets against quantum computers. We’ve added a requirement for a second stamp with stronger magic, this magic cannot be reversed by a quantum computer.

Community Buzz

What industry leading companies are saying

Lamport Signatures Prof Bill Buchanan OBE

Lamport Signatures for a Post-Quantum Computing World: Towards a More Trusted Quantum Computing World
Jay Gambetta IBM Quantum VP - IBM

What IBM has to say

Simone Severini Director, Quantum Computing - AWS

What Amazon has to say

    Community Buzz

    What industry leaders are saying

    Hartmut Neven Engineering Director - Google

    Id felis ut senectus platea cubilia. Ac litora pretium pellentesque elementum lacus sem arcu justo curae. Mus fermentum habitant conubia pede consectetuer.

    Jay Gambetta IBM Quantum VP - IBM

    Id felis ut senectus platea cubilia. Ac litora pretium pellentesque elementum lacus sem arcu justo curae. Mus fermentum habitant conubia pede consectetuer.

    Simone Severini Director, Quantum Computing - AWS

    Id felis ut senectus platea cubilia. Ac litora pretium pellentesque elementum lacus sem arcu justo curae. Mus fermentum habitant conubia pede consectetuer.

      FAQ

      Frequently Ask Questions

      Lorem ipsum dolor sit amet, consectetur adipiscing elit.

      Quantum computers are physical devices that harness the laws of quantum mechanics to efficiently solve some types of problems that would otherwise take ages on machines designed to operate only from classical physics principles.

      Quantum computers will have the ability to recover the private keys from the public keys stored on blockchains. Almost all blockchains use elliptic curve cryptography for signing transactions on a ledger. While elliptic curve cryptography cannot be hacked with a classical computer, it is one of the easiest methods to break with a large enough quantum computer using Shor's discrete logarithm algorithm.
      secp256k1 refers to the parameters of the elliptic curve used in Bitcoin's public-key cryptography, and is defined in Standards for Efficient Cryptography (SEC) (Certicom Research, http://www.secg.org/sec2-v2.pdf). Currently Bitcoin uses secp256k1 with the ECDSA algorithm, though the same curve with the same public/private keys can be used in some other algorithms such as Schnorr.

      secp256k1 was almost never used before Bitcoin became popular, but it is now gaining in popularity due to its several nice properties. Most commonly-used curves have a random structure, but secp256k1 was constructed in a special non-random way which allows for especially efficient computation. As a result, it is often more than 30% faster than other curves if the implementation is sufficiently optimized. Also, unlike the popular NIST curves, secp256k1's constants were selected in a predictable way, which significantly reduces the possibility that the curve's creator inserted any sort of backdoor into the curve.
      P2PK addresses on Bitcoin (for which the public key is recorded on the blockchain) are at imminent risk.
      The Pauli Group solution: assess the risk empirically with application benchmark challenges that can be used to measure the progress of the large-scale integration of quantum computing systems. Specifically, these benchmarks will take the form of challenge for near- and mid-term fault-tolerant devices meant to quantitatively assess the risks of cryptographic assets.

      Want to secure your digital assets from quantum computers and remain in control of your keys?

      Create your Anchor Wallet today!

      Create Wallet

      Join us on Discord

      Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

      Resources

      Organization

      Free Resources

      Sign up for insights and free resources to level-up!
      Linkedin-in Twitter
      Copyright © 2023 Pauli Group. All rights reserved.